Determine os esforços seccionais da viga pré-fabricada em concreto armado do Exemplo 1.8 do primeiro capítulo.
Passo 1
Fala ae, pessoal! Tudo bem?
Sabemos que o peso específico da estrutura é de
A área da seção transversal é
Fazendo , temos a carga distribuída que atua na estrutura:
Passo 2
O exemplo 1.8 nos dá o valor da força atuante em cada cabo
Só que e são forças inclinadas, portanto:
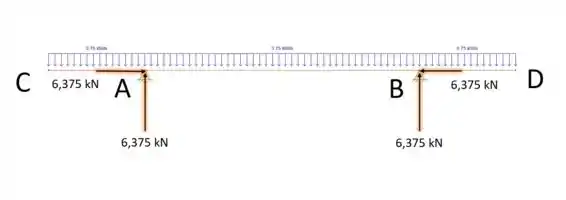
Abaixo temos uma representação da estrutura:
Passo 3
Calculando os esforços internos vindo pela esquerda, temos:
Passo 4
Entre os pontos e temos um momento máximo, devido à simetria da estrutura ele ocorre na metade do segmento. Logo:
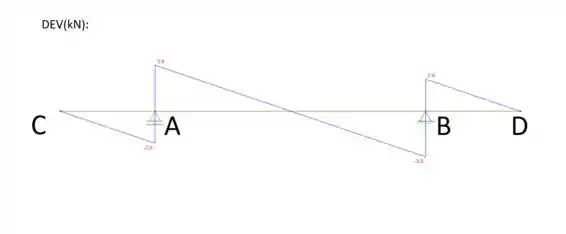
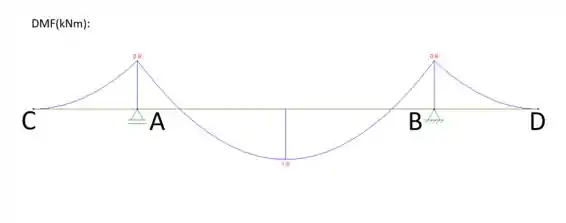
Portanto, os diagramas da viga de concreto armado são:

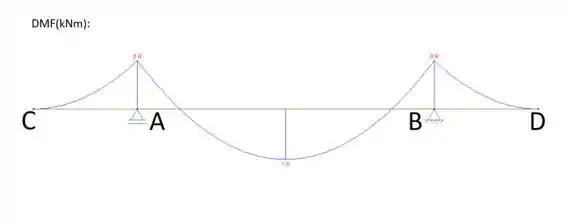
Resposta