Determine as forças nas barras DE e AE da treliça da figura
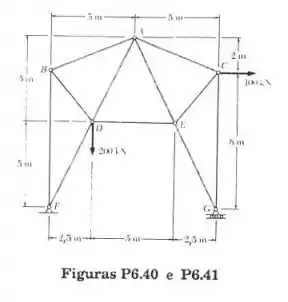
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Desenhe o diagrama de corpo livre da treliça
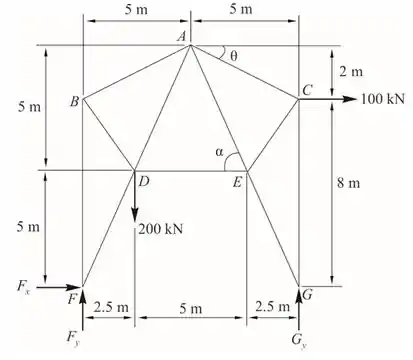
Passo 2
Calcularemos os ângulos mostrados no diagrama de corpo livre
Tomemos momentos sobre F
Passo 3
Considere uma porção do lado direito da seção que passa pelos membros CA, EA e ED conforme mostrado na figura:
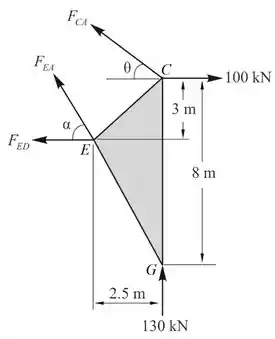
Passo 4
Tome momentos sobre E:
Da equação de equilíbrio ao longo do eixo y:
Portanto, a força no membro EA é .
Da equação de equilíbrio ao longo do eixo de x:
Portanto, a força no membro ED é .
Resposta
Portanto, a força no membro EA é .
Portanto, a força no membro ED é .