Determine as forças resultantes nos pinos A, B e C da treliça de telhado em arco tri articulado.
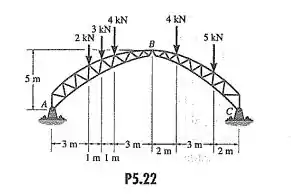
Passo 1
E ai meus queridos, tudo dentro dos eixos?
Haha
Bora resolver essa comigo?
Encostaaa
Já vamos iniciar com o nosso diagrama da treliça
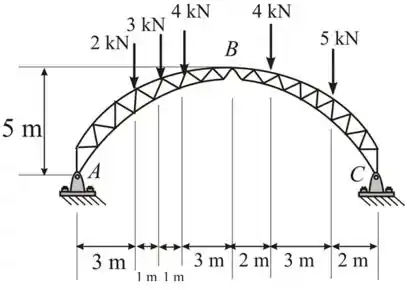
Passo 2
Vamos considerar a parte AB e redesenhar esse diagrama
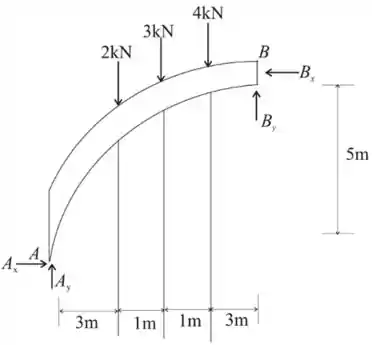
Vamos tomar o momento sobre A
Passo 3
Agora iremos considerar a parte BC e redesenhar o nosso diagrama
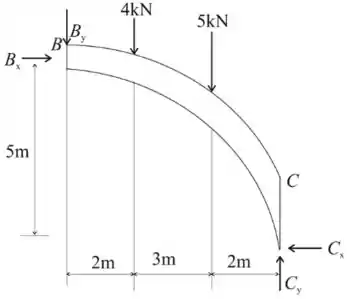
Tomando o momento sobre C, teremos
Agora resolvendo as duas equações a seguir, iremos obter:
(Observação: podemos resolver por matrizes, cramer, escalonamento, ou de algum outro método que achar fácil).
Passo 4
Para o membro AB, nós temos
Para o membro BC, temos
Passo 5
A força resultante no pino A
A força resultante no pino B.
A força resultante no pino C.