Determine a frequência das pequenas oscilações de uma placa fina homogênea caso o movimento ocorra no plano da placa e caso a placa tenha a forma de um triângulo equilátero e se encontre suspensa (A) pelo ponto médio de um lado e (B) por um vértice.
Passo 1
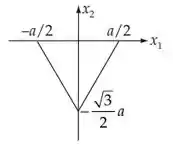
A área do triângulo é , então a densidade será:
Passo 2
A inércia rotacional em relação a um eixo que passa pelo ponto de suspensão (a origem) é:
Quando o triângulo está suspenso como quando , as coordenadas do centro de massa
são, onde:
A energia cinética será:
E a energia potencial:
Portanto:
Onde o termo constante pode ser suprimido. A equação de Lagrange para é:
E para pequenas oscilações, a frequência é:
E essa é a resposta da letra A.
Passo 3
A inércia rotacional para um eixo através do ponto de suspensão para este caso é:
A Lagrangiana agora será:
E a equação do movimento:
Assim a frequência para pequenas oscilações é:
E essa é a resposta da letra B. Que é levemente menor que o resultado da letra A.
Resposta
Ei, a resposta está no passo a passo :)