Determine a hamiltoniana e as equações de movimento de Hamilton para (a) um pêndulo simples e (b) uma máquina de Atwood simples (polia simples).
Passo 1
Faaaaaala, galera... Tranquileba??
Para a)

Um pendulo simples não é segredo pra gente. Sabemos que as coordenadas xy são:
Assim, energias são dadas por:
E a lagrangiana é:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim, o momento mecânico em relação ao é:
Desde que a energia U seja independente do tempo, a Hamiltoniana é a energia total:
E as equações de movimento são:
Passo 3
Para b)
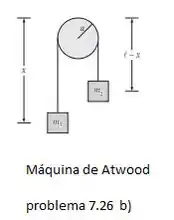
Assim, a energia cinética (que também conter o movimento rotacional) é:
E a energia potencial é:
Assim a lagrangiana é:
De forma que o momento mecânico é:
De forma que:
Desde que U não dependa do tempo, a energia total é a hamiltoniana:
E as equações de movimento são:
Resposta
Para a)
Para b)