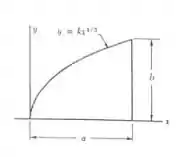
Determine, por integração direta, o momento de inércia da superfície sombreada, em relação ao eixo de x.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Vamos encontrar o valor de k para a equação
Logo
Passo 2
Agora iremos visualizar o nosso D.C.L da área sombreada
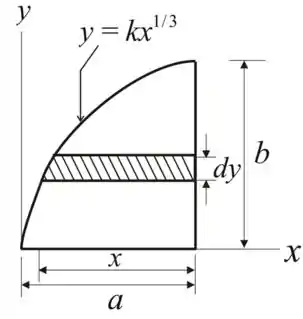
Vamos considerar uma tira elementar dx para a figura dada.
A área da faixa elementar do retângulo é
O momento de inércia da área elementar é
Agora iremos resolver a expressão (1) para o valor de x
Substituindo o valor de x na expressão (2), temos
Passo 3
Resolva a equação acima para o momento de inércia
Resposta
Portanto, o momento de inércia da área sombreada em relação ao eixo de x é .