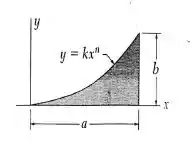
Determine, por integração direta, o momento de inércia da superfície sombreada, em relação ao eixo x.
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
Iremos encontrar o valor de k da equação
Portanto, a equação 1, acaba se tornando
Passo 2
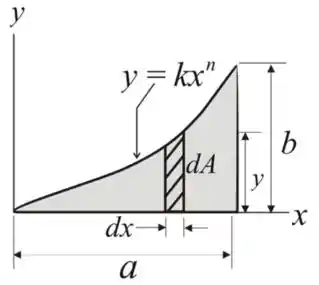
Agora iremos desenhar o D.C.L da área sombreada, como mostra a seguir
Passo 3
Vamos considerar uma tira elementar para a figura que foi dada no passo anterior
A área da faixa elementar é
O momento de inércia da área elementar é
Resolvendo, temos:
Resposta
Portanto, o momento de inércia da área sombreada em relação ao eixo x, é de