Determine, por integração direta, o momento de inércia da superfície sombreada, em relação ao eixo y.
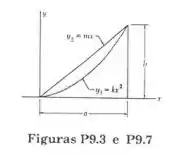
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Vamos considerar um elemento diferencial paralelo ao eixo y como mostrado a seguir
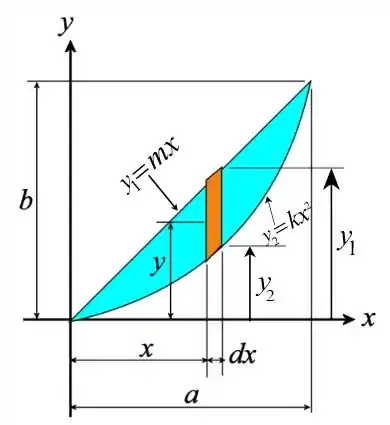
Passo 2
Determinando as constantes das duas curvas
Considerando
Considerando
Passo 3
Vamos escrever a expressão para a área elementar
Resposta
Portanto, o momento de inércia da área sombreada em relação ao eixo y, é de