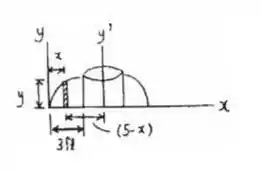
Determine o momento de inércia do objeto formado girando a área sombreada em torno da linha x = 5 pés. Expresse o resultado em termos da densidade do material, ρ.
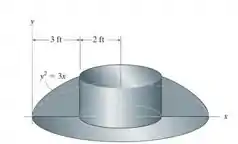
Passo 1
O enunciado gurizada pede que a gente determine o momento de inércia do objeto formado girando a área sombreada em torno da linha x = 5 pés. Expresse o resultado em termos da densidade do material, ρ.
]
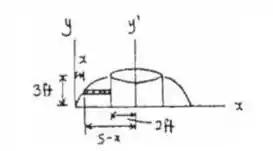
Passo 2
Massa do corpo
Passo 3
Também