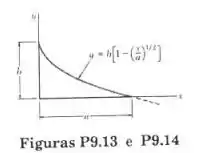
Determine o momento de inércia e o raio de giração da superfície sombreada da figura, em relação ao eixo y.
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
A equação para a parte sombreada é
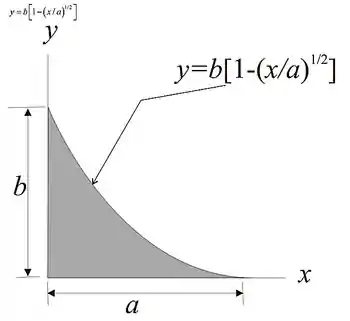
Seguido do D.C.L
Passo 2
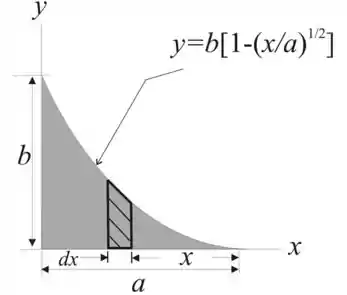
Vamos considerar uma tira elementar dx para a figura dada.
A área da faixa elementar é
O momento de inércia da área elementar é
Passo 3
Integrando a equação, teremos
O raio de giração é