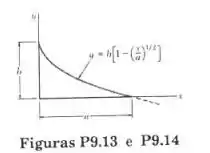
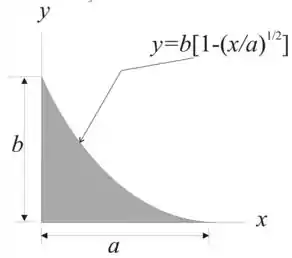
Determine o momento de inércia e o raio de giração da superfície sombreada da figura, em relação ao eixo x.
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Para a equação dada
Os limites são
A área total da curva é
Passo 2
Vamos considerar uma tira elementar dx para a figura dada.
A área da faixa elementar é
O momento de inércia da área elementar é
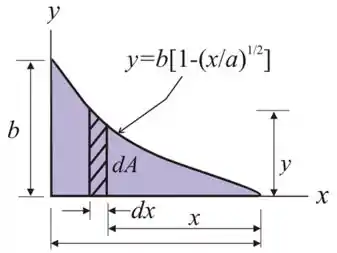
Integrando
Portanto, o momento de inércia da área sombreada em relação ao eixo y é .
Passo 3
Vamos encontrar o raio de giração da área sombreada usando a seguinte equação
Resposta
Portanto, o momento de inércia da área sombreada em relação ao eixo y é .
Portanto, o raio de giração é .