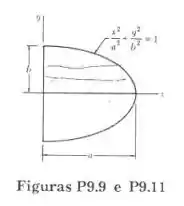
Determine o momento de inércia e o raio de giração da superfície sombreada ilustrada, em relação ao eixo x.
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Já iremos iniciar desenhando o diagrama mostrando o elemento diferencial vertical
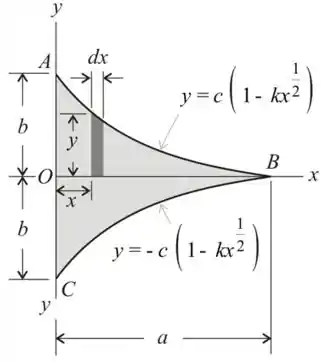
A figura é simétrica em relação ao eixo x
Para uma tira elementar, o momento de inércia em relação ao eixo x é dado como
Portanto, o momento de inércia da seção AOB em torno do eixo x é dado como
Passo 2
A equação da curva fica da seguinte maneira
No ponto A
Substituindo os valores acima na expressão (2)
No ponto b
Substituindo os valores acima na expressão (2)
Passo 3
Substituindo a equação (3) e (4) na expressão (2), temos
Substituindo a equação (5) na equação (1)
Aplicando o limite de 0 a a
Calcule o momento de inércia total da região sombreada em relação ao eixo x
Resposta
Portanto, o momento de inércia da região sombreada em torno do eixo x é .