Determine o momento de inércia e o raio de giração da superfície sombreada em relação ao eixo x.
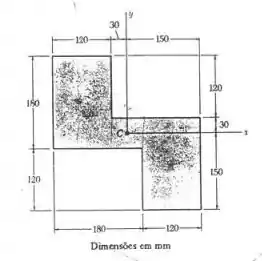
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
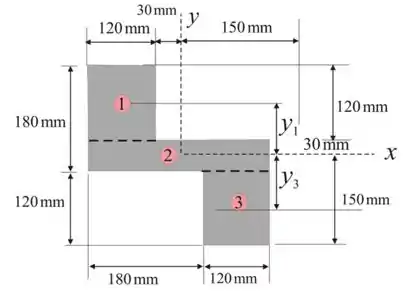
Vamos dividir nossa área em 3 retângulos como mostra a figura a seguir
Vamos considerar a seguinte figura como retângulo 1
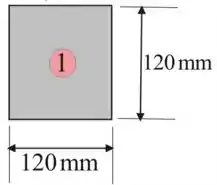
Iremos encontrar o momento de inércia para a porção retangular 1 usando a seguinte expressão
Passo 2
Considerando o segundo triangulo
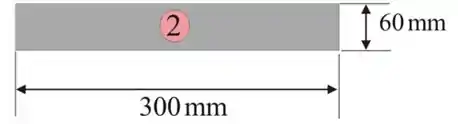
Iremos encontrar o momento de inércia para a porção retangular 2 usando a seguinte expressão
Considerando o retângulo 3
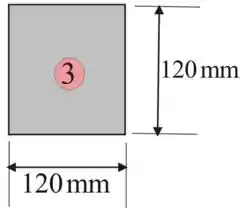
Iremos encontrar o momento de inércia para a porção retangular 3 usando a seguinte expressão
Passo 3
Encontre o momento de inércia da área total em relação ao eixo x usando a relação seguinte
Portanto o momento de inércia total em torno do eixo x é de .
Encontraremos o raio de giração da área sombreada usando a seguinte expressão
Portanto, o raio de giração é .
Resposta
Portanto o momento de inércia total em torno do eixo x é de .
Portanto, o raio de giração é .