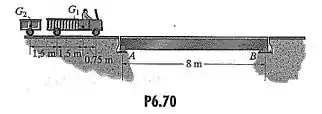
Determine o momento máximo absoluto na ponte no Problema 6.69 se o reboque for removido.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Vamos começar convertendo a massa em Newton usando a seguinte expressão
O R resultante para a condição de carregamento como segue
Passo 2
Distribua a carga que atua entre os dois pontos finais de acordo com a distância de
Vamos considerar a figura a seguir
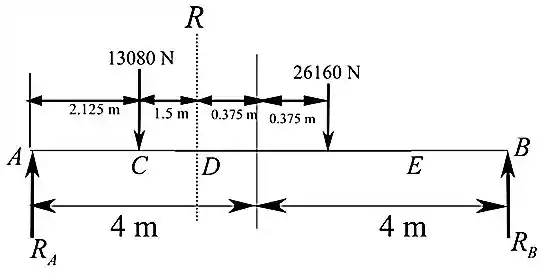
Passo 3
Vamos calcular o momento máximo absoluto da seguinte maneira:
Tomemos o momento sobre A:
Passo 4
Considerando a figura a seguir
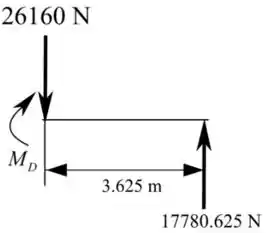
Agora iremos calcular o momento em D sob a carga de 13080 N como mostrarei a seguir:
Portanto, o momento máximo absoluto é .
“A única maneira de saber o quão forte você é, é continuar testando seus limites” (Superman) .
Resposta
Portanto, o momento máximo absoluto é .