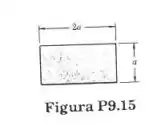
Determine o momento polar de inércia e o raio de giração polar do retângulo ilustrado, em relação ao ponto médio de um de seus (a) maiores lados (b) menores lados.
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Vamos iniciar desenhando o diagrama da área
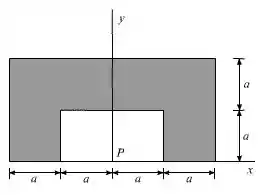
Iremos calcular o momento de inércia do retângulo externo em relação ao eixo x
Passo 2
Vamos calcular o momento de inércia do retângulo interno em relação ao eixo x
Calculando o momento de inércia da área sombreada em torno do eixo x. Considerando a seguinte expressão
Calculando o momento de inércia do retângulo externo em torno do eixo y, temos
Calculando o momento de inércia do retângulo interno em torno do eixo y, temos
Calculando o momento de inércia da área sombreada em torno do eixo y. Considerando a seguinte expressão
Passo 3
Calculando o momento de inércia polar da área sombreada em relação ao ponto P. Consideremos o teorema do eixo perpendicular
Portanto, o momento polar de inércia da área sombreada em relação ao ponto P é .
A área da região sombreada é
Vamos calcular o raio de giração polar da área sombreada em torno do ponto P
Portanto, o raio polar de giração da área sombreada em relação ao ponto P é .
Resposta
Portanto, o momento polar de inércia da área sombreada em relação ao ponto P é .
Portanto, o raio polar de giração da área sombreada em relação ao ponto P é .