Determine o momento polar de inercia e o raio polar de giração do trapézio ilustrado em relação ao ponto .
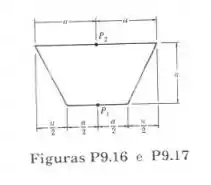
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Então já iremos iniciar com o diagrama
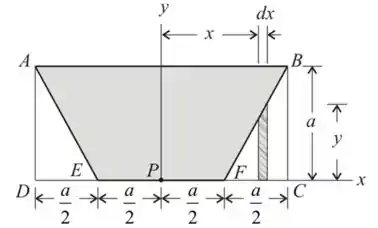
Calculando a área do trapézio
Vamos calcular o momento de inércia do retângulo ABCD em relação ao eixo x
Vamos calcular o momento de inércia do retângulo BCF em relação ao eixo x
Vamos calcular o momento de inércia do retângulo ADE em relação ao eixo x
Passo 2
Vamos calcular o momento de inércia da área sombreada em torno do eixo x.
Usando o teorema dos eixos paralelos e desloque o momento de inércia em relação ao ponto , temos
Vamos calcular o momento de inércia do retângulo ABCD em relação ao eixo y
Suponhamos que a equação da linha BF como,
As coordenadas do ponto F são
Substituindo as coordenadas do ponto F da equação (1) e determinaremos a relação para constante
Passo 3
As coordenadas do ponto B são
Substituindo
Portanto, a constante é
Finalmente a equação torna – se
Calculando o momento de inércia do triângulo BCF em torno do eixo y, temos
Passo 4
Por simetria da figura, o momento de inércia do triângulo ADE em relação ao eixo y, temos
O momento de inércia da área sombreada em torno do eixo y, é
Calcularemos o momento polar de inércia da área sombreada em relação ao ponto P
Portanto, o momento polar de inércia da área sombreada em relação ao ponto Pé
Passo 5
Calculando a área da seção
Além disso, o momento polar de inércia da área sombreada é
Portanto, o raio polar de giração da área sombreada em relação ao ponto P é .
Resposta
Portanto, o momento polar de inércia da área sombreada em relação ao ponto P é
Portanto, o raio polar de giração da área sombreada em relação ao ponto P é .