Determine a posição do centroide a área plana da figura.
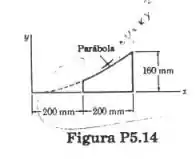
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
Já iremos desenhar a área sombreada para melhor visualização
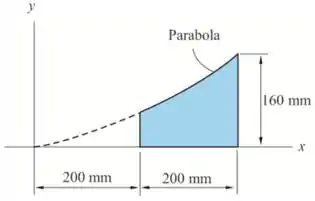
Passo 2
A área sombreada dada é obtida pelas seguintes áreas
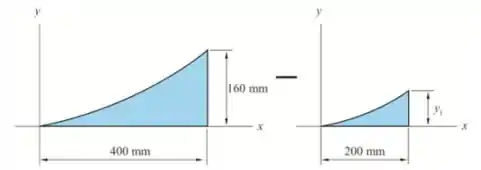
Passo 3
Pela equação da curva parabólica temos
Temos
Substituindo na equação da curva
Em
Os primeiros momentos das áreas componentes em relação aos eixos de coordenadas serão calculados e inseridos na tabela, como mostra a seguir:
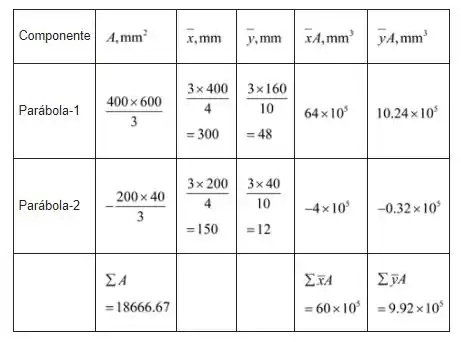
Passo 4
A coordenada x do centroide da área sombreada é feita da seguinte maneira
Portanto, a coordenada x do centroide da área sombreada é .
A coordenada y do centroide da área sombreada é feita da seguinte maneira
Portanto, a coordenada y do centroide da área sombreada é
Resposta
Portanto, a coordenada x do centroide da área sombreada é .
Portanto, a coordenada y do centroide da área sombreada é