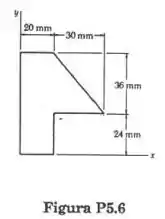
Determine a posição do centroide da superfície plana da figura.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
A área do membro é obtida pela soma da área do retângulo e do triângulo
Passo 2
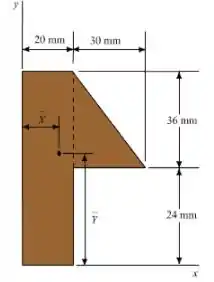
Usando os eixos de coordenadas, a área e as coordenadas do centroide de cada uma das áreas componentes são determinadas

Passo 3
Nós temos conhecimento sobre:
Substituindo os valores conhecidos na expressão
Portanto, o centroide na componente x, é .
Sabemos também sobre:
Substituindo os valores conhecidos na expressão
Portanto, o centroide na componente y, é .
Resposta
Portanto, o centroide na componente x, é .
Portanto, o centroide na componente y, é .