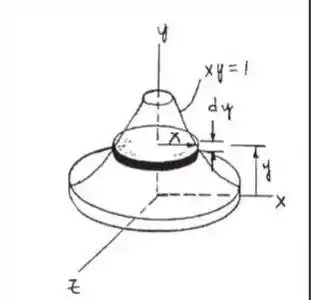
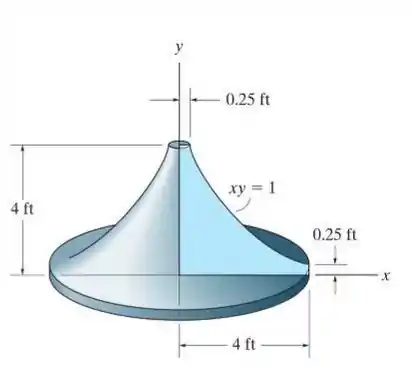
Determine os raios de giração e para o sólido formado girando a área sombreada em torno do eixo y. A densidade do material é ρ.
Passo 1
O enunciado gurizada pede que a gente determine os raios de giração e para o sólido formado girando a área sombreada em torno do eixo y. A densidade do material é ρ.
Para A massa do elemento diferencial é
Passo 2
Portanto
Por isso
Para
Por isso