Determine as reações de apoio dos pórticos planos esquematizados na próxima figura.
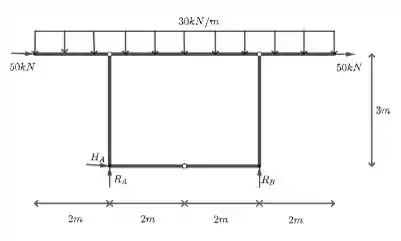
Passo 1
Primeiramente, vamos identificar as reações presentes nesse pórtico. No ponto A, temos uma reação horizontal e uma vertical, enquanto no ponto B temos somente a reação horizontal. Como temos mais incógnitas atuando no ponto A, esse é o ponto mais conveniente para utilizar a equação de equilíbrio dos momentos das forças. Isso vai ficar mais claro mais adiante.
Forças horizontais:
Além da reação horizontal temos também duas forças horizontais de módulo , uma atuando à esquerda e outra à direita, a do solo. Por serem horizontais, somente a distância vertical dessas forças até o ponto A () vai importar para o cálculo dos momentos.
Forças verticais:
Além das reações e , temos uma força de uniformemente distribuída por . Essa força é equivalente a uma força de módulo aplicada no ponto . Esse ponto está a uma distância horizontal de do ponto A. Além disso, está a do ponto A.
Passo 2
Agora com as forças identificadas, podemos utilizar as equações de equilíbrio:
O sinal negativo indica que aponta no sentido negativo de .