Determine as reações de apoio das vigas representadas na próxima figura.
Passo 1
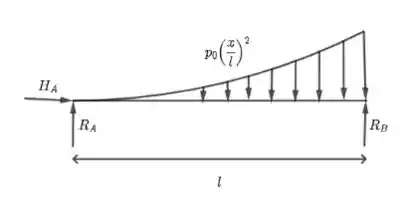
No apoio A, temos uma reação vertical e uma horizontal. Como não há forças horizontais, então . No apoio B, que está a uma distância de A, temos somente a reação vertical. Vamos calcular os momentos com relação a A.
O segredo aqui é descobrir a força que tem efeito equivalente ao da força distribuída e seu ponto de aplicação:
.
Logo, o efeito da força distribuída é equivalente a aplicar uma força de módulo no ponto .
Passo 2
Agora, aplicamos essas forças nas equações de equilíbrio: