Determine as reações de apoio das vigas representadas na próxima figura.
Passo 1
Vamos tomar o ponto A como referência para calcular os momentos das forças. Primeiramente, identificamos as forças:
A força de reação em B está a do ponto A. A força de está a em relação a viga e a do ponto A. Logo, tem componentes
A força distribuída de é equivalente a aplicar uma força
a uma distância do ponto A. Temos duas forças de , uma que está no ponto A (logo não gera momento da força) e uma a uma distância do ponto A. Além disso, a força de reação horizontal aponta na direção . O diagrama de corpo livre está esquematizado abaixo:
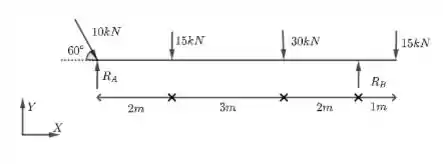
Passo 2
Agora, podemos aplicar as equações de equilíbrio:
O sinal negativo indica que aponta na direção negativa de .