Determine as reações de apoio das vigas representadas na próxima figura.
Passo 1
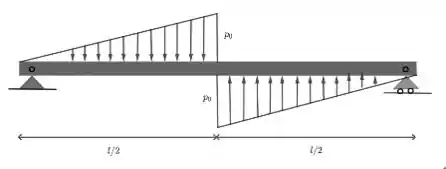
No primeiro apoio, que chamaremos de A, temos uma reação vertical e uma horizontal. Como não há forças horizontais, podemos concluir que . No segundo apoio, B, está a uma distância de A e tem somente a reação vertical. Vamos calcular os momentos com relação a A.
A força distribuída na primeira metade viga tem módulo máximo em . Assim, essa força é equivalente a aplicar uma força de módulo , no ponto . Essas fórmulas foram demonstradas no exercício 2 viii, então se você ficou com dúvida, dá uma olhadinha lá.
A força distribuída na segunda metade vai ter os mesmos valores, mas agora temos que prestar atenção que é a distância até a extremidade direita (ponto B). Então a distância do ponto de aplicação da força equivalente até A é na verdade . Além disso, essa força aponta no sentido positivo de .
Passo 2
As equações de equilíbrio nos dão:
.
O sinal negativo quer dizer que aponta no sentido negativo de .