Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 5.5 - Ex. 14

Determine a tensão fletora máxima σ m á x (devido á flexão pura por um momento M), para uma viga com seção circular na forma de uma parte central de um circulo (veja a figura). O círculo tem diâmetro d e ângulo β = 60 ° .(Dica : Utilize as fórmulas do Apêndice D, Casos 9 e 15).

Passo 1

Fala meus queridx’sss , BORA LÁ!!

Primeiro passo e essa belezinha de D.C.L.

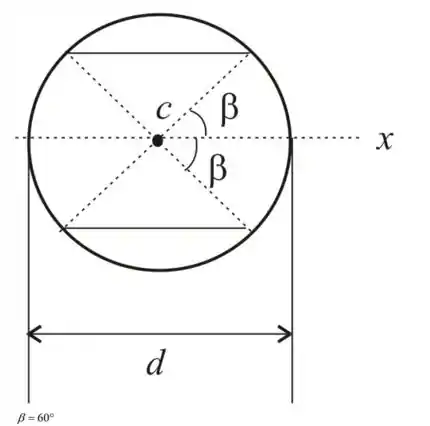
Passo 2

Pelas propriedades nas tabelas de área os valores dados são

I x = π r 4 4 - r 4 2 ( α - a b r 2 + 2 a b 3 r 4 )

r = d 2

α = π 2 - β

α = r   s e n   β

b = r cos ⁡ β

Passo 3

I x = π d 4 64 - d 4 32 π 2 - β - s e n β c o s β + 2 s e n β cos 3 ⁡ β

I x = π d 4 64 - d 4 32 π 2 - β - s e n β c o s β 1 - 2 cos 2 ⁡ β

I x = π d 4 64 - d 4 32 π 2 - β - 1 2 s e n 2 β - c o s 2 β

I x = π d 4 64 - d 4 32 π 2 - β + 1 4 s e n   4 β

I x = d 4 128 ( 4 β - s e n 4 β )

Passo 4

A tensão máxima de flexão

σ m á x = M c I c

Distância centroide

c = r   s e n   β

σ m á x = 64 M   s e n β d 3 4 β - s e n   4 β

Para

β = π 3 = 180 3 = 60 °

σ m á x = 64 M   s e n 60 ° d 3 4 × π 3 - s e n   4 × 60 °

σ m á x = 576   M 8 π 3 + 9 d 3

σ m á x = 10.96 M d 3

Resposta

Vide o passo a passo.