Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 108

Determine o valor de a para o qual o momento máximo positivo tenha o mesmo valor que o momento máximo negativo. EI é constante.

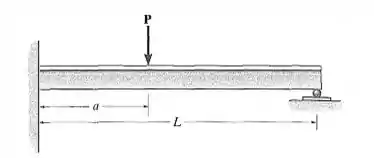
Passo 1

Fala aí pessoal, partiu mais um problema de resmat. Este problema pede o valor de a para que os momentos positivo e negativo tenham o mesmo valor em módulo. Vamos fazer o somatório de momentos em A:

∑ M a = 0 → - M A + B y L - P a = 0

∑ F y = 0 → A y + B y - P = 0

As equações do momento são:

M x 1 = A y x 1 + M A → 0 ≤ x 1 ≤ a

M ( x 2 ) = A y x 2 - P x 2 + P a + M A

Sabemos que:

E I d v 2 d x 2 = M x

Integrando-se duas vezes as equações do momento, temos:

E I v 1 = A y 6 x 1 ³ + M A x 1 2 2   C 1 x 1 + C 2

E I v 2 = A y 6 x 2 ³ - P 6 x 2 ³ + P a 2 x 2 ² +   C 3 x 2 + C 4

Para a determinação das constantes, temos que aplicar as condições de contorno. As condições de contorno são:

x 1 = 0 → v 1 = 0  

x 2 = L →   v 2 = 0

x 1 = x 2 = a → d v 1 d x 1 = d v 2 d x 2

Logo:

C 1 = 0

C 2 = 0

C 3 = - P a 2 2

C 4 = P a 2 L 2 - P a L 2 2 + P L 3 6 - A y L 3 6 - M L 2 2

Passo 2

Agora vamos utilizar alguns pontos para determinar as reações:

x 1 = x 2 = a → v 1 = v 2

M A = P L 3 + 3 P a 2 L - 3 P a L 2 - P a 3 - A y L 3 3 L 2

Substituindo de novo para achar a reação em A:

A y = P 2 L 3 2 L 3 - 3 a 2 L + a 3

B y = P - P 2 L 3 2 L 3 - 3 a 2 L + a 3

Substituindo na equação do momento em A:

M A = P a 2 L 2 3 a L - a 2 - 2 L 2

Este é o momento negativo.

O positivo será:

M = A y a + M A

Se igualarmos os 2, ficamos com:

a = 2 - 2 L

Resposta

a = 2 - 2 L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga está sujeita à carga mostrada na figura. Determine a inclinação em A e o deslocamento em C. EI é constante
Determine a equação da linha elástica. Especifique a inclinação em A e o deslocamento em C. EI é constante
Determine a equação da linha elástica. Especifique a inclinação em A e B. EI é constante
Determine a equação da linha elástica. Especifique a deflexão em C
Determine a equação da linha elástica. Especifique a inclinação em B