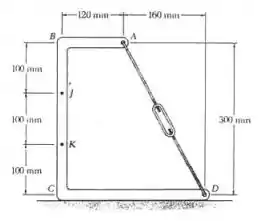
Determinou-se experimentalmente que o momento fletor no ponto K da estrutura da figura é . Determine : (a) a tração no fio AD e (b) a correspondente força interna no ponto J
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
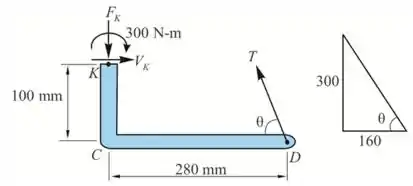
Vamos considerar o seguinte D.C.L de DK
Passo 2
- Pela figura
Tomemos momentos sobre K
Portanto, a tensão no fio AD é de
Passo 3
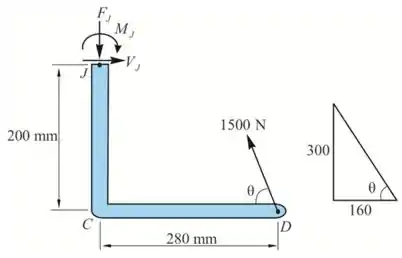
Iremos considerar o D.C.L de JD
Passo 4
Da equação de equilíbrio ao longo do eixo de x
Portanto, a força cortante em J no membro JD é de
Da equação de equilíbrio ao longo do eixo de y
Portanto, a força normal em J no membro JD é de
Tomando momentos sobre J
Portanto, o momento fletor em J no membro JD é de
Resposta
- Portanto, a tensão no fio AD é de
- Portanto, a força normal em J no membro JD é de .
Portanto, o momento fletor em J no membro JD é de
Portanto, a força cortante em J no membro JD é de .