Um disco homogêneo de raio R e massa M rola sem escorregar sobre uma superfície horizontal e é atraído para um ponto a uma distância d abaixo do plano. Se a força de atração é proporcional à distância do centro de massa do disco ao centro de força, determine a frequência de oscilações em torno da posição de equilíbrio.
Passo 1
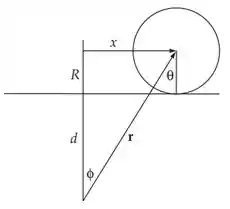
Conforme a figura a força entre o centro de força e o disco é:
Passo 2
Apenas a componente no eixo execerce trabalho, logo a força resultante:
E isso corresponde a uma energia potencial , daí a energia cinética do disco será:
Passo 3
Onde nós usaremos o resultado para um disco e . A equação de Lagrange nos dá:
Resposta
E esse é um movimento harmônico simples sobre com uma frequência angular de oscilação no valor de: