Um disco roda sem deslizar por um plano horizontal. O plano do disco permanece vertical, mas está livre para girar sobre um eixo vertical. Quais coordenadas generalizadas podem ser utilizadas para descrever o movimento? Formule uma equação diferencial que descreve uma restrição de rodagem. Esta equação é integrável? Justifique sua resposta com um argumento físico. A restrição é holonômica?
Passo 1
Faaaaaala, galera... Tranquileba??
Fazendo um esboço da situação, temos:
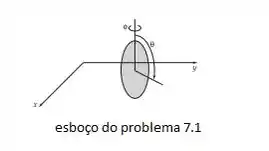
Quatro coordenadas são necessárias para descrevermos o movimento, isto é:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Desde que o disco role apenas em uma direção, nós temos ter apenas as seguintes condições:
Passo 3
Veja que essas equações não são integrais, e porque nós não podemos obter umaequação que relacione as coordenadas, as restrições são não- holonômica, dde forma que não haja uma equação precisa que determine a posição.
Resposta
Ei, a resposta está no passo a passo :)