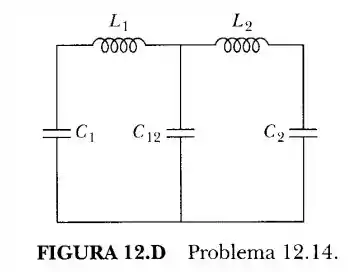
Discuta os modos normais do sistema mostrado na Figura 12.D.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações acopladas.
O esquema do problema apresentado, com o sentido adotado da aplicação da lei das malhas:
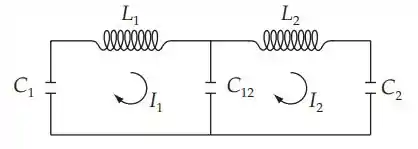
As equações do circuito de Kirchhoff, depois de diferenciar usando , são:
Usando uma dependência de tempo harmônico para , a equação encontrada é:
Resolvendo para a frequência:
Como as frequências características são dadas por essa expressão complicada, examinamos os modos normais para o caso especial em que L1 = L2 = L e C1 = C2 = C. Então:
Observe que ω2 corresponde ao caso de oscilações desacopladas. As equações para este circuito simplificado podem ser definidas da mesma forma que a Eq. (12.1), e consequentemente os modos normais podem ser encontrados da mesma forma que na Seção 12.2. Haverá dois modos possíveis de oscilação: (1) fora de fase, com frequência ω1, e (2) em fase, com frequência ω2.
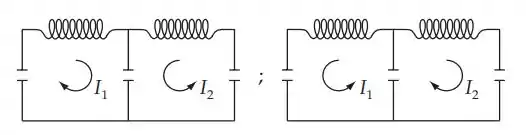
O modo 1 corresponde às correntes I1 e I2 oscilando sempre fora de fase:
O modo 2 corresponde às correntes I1 e I2 oscilando sempre em fase:
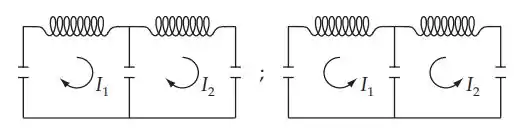
(A analogia com dois osciladores acoplados por uma mola pode ser vista associando o caso 1 com a Fig. 12-2 para ω = ω1 e o caso 2 com a Fig. 12-2 para ω = ω2). Se agora temos e , não temos modos simétricos e antissimétricos puros, mas podemos associar ω2 com o modo de maior grau de simetria e ω1 com o de menor grau de simetria.
Resposta
Ver passo a passo.