Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 1.2 - Ex. 5

Dois cabos de aço, A B e B C , sustentam uma lâmpada pesando 15   l b (veja a figura). O cabo A B está em um ângulo de α = 35 ° com a horizontal e o cabo B C está em um ângulo de β = 50 ° . Ambos os cabos têm diâmetro de 25   m i l s . (O diâmetro de um cabo é geralmente expresso em m i l s : um mil é igual a 0,001   i n ). Determine as tensões de tração σ A B e σ B C nos dois cabos.

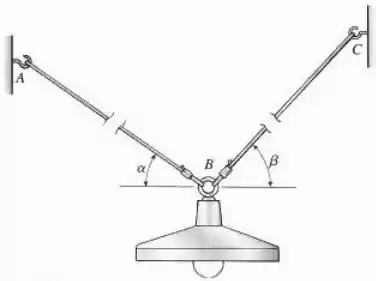
Passo 1

Bora lá galera!

Dados:

α = 35 °

β = 50 °

d = 2,5   m i l s = 0,025   i n

W = 15   l b

A = π 4 d 2 = π 4 ⋅ 0,025 2 = 4,91 ⋅ 10 - 4   i n 2

Fazendo o somatório das forças em x, temos:

∑ F x = 0

- T A B cos ⁡ α + T B C cos ⁡ β = 0

Fazendo o somatório das forças em y, temos:

∑ F y = 0

T A B sen ⁡ α + T B C sen ⁡ β - W = 0

Com isso my friends, substituindo os valores, nós conseguimos montar o seguinte sistema:

- T A B cos ⁡ 35 + T B C cos ⁡ 50 = 0 T A B sen ⁡ 35 + T B C sen ⁡ 50 - 15 = 0

E resolvendo o sistema, encontramos que:

T A B = 9,679   l b

T B C = 12,334   l b

Passo 2

Como a questão pede as tensões de tração, basta apenas substituirmos os valores, logo:

σ A B = T A B A = 9,679   4,91 ⋅ 10 - 4 = 19712,83   p s i

σ B C = T B C A = 12,334   4,91 ⋅ 10 - 4 = 25120,16   p s i

Essa questão foi, heim... Bora pra próxima?

Resposta

σ A B = 19712,83   p s i

σ B C = 25120,16   p s i