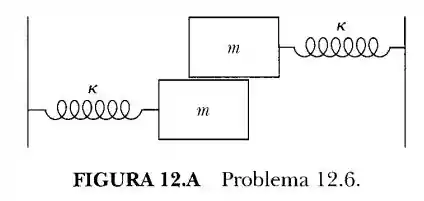
Dois osciladores harmônicos idênticos são posicionados de tal maneira que as duas massas deslizem uma contra a outra, como na Figura 12.4. A força de atrito proporciona um acoplamento dos movimentos proporcional à velocidade relativa instantânea. Discuta as oscilações acopladas do sistema.

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações acopladas.

O esquema do problema apresentado:

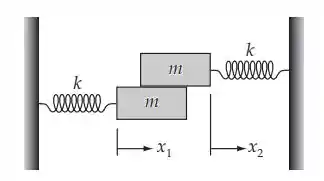
Se a força de atrito agindo na massa 1 devido à massa 2 é:

Então as equações do movimento são:

Como o sistema não é conservativo, as frequências próprias não serão inteiramente reais como nos casos anteriores. Portanto, tentamos uma solução da forma:

Onde α = λ +iω é uma quantidade complexa a ser determinada.

Substituindo em f, obtemos a seguinte equação:

De onde encontramos as duas soluções:

A solução geral é, portanto:

E da mesma forma para x2(t).

Os dois primeiros termos na expressão para x1(t) são puramente oscilatórios, enquanto os dois últimos termos contêm o fator de amortecimento . (Observe que o termo aumenta com o tempo se β2 > mκ , mas não precisa desaparecer para produzir movimento fisicamente realizável porque o termo de amortecimento, exp(–βt), diminui com o tempo a uma taxa mais rápida; que é ).

A quais modos α1 e α2 se aplicam?

No modo 1 há movimento puramente oscilante sem atrito. Isso só pode acontecer se as duas massas não tiverem movimento relativo. Assim, o modo 1 é o modo simétrico em que as massas se movem em fase.

O modo 2 é o modo antissimétrico no qual as massas se movem fora de fase e produzem amortecimento por atrito. Se β2 mκ, o movimento prossegue monotonicamente para amplitude zero.