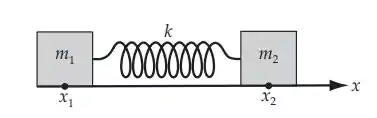
Duas massas m1 = 100 g e m2 = 200g deslizam livremente em uma pista horizontal sem atrito e são conectadas por uma mola cuja constante de força é k = 0,5 N/m. Determine a frequência do movimento oscilatório desse sistema.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações.
Suponha que as coordenadas de m1 e m2 sejam x1 e x2 e o comprimento da mola no equilíbrio seja l. Então as equações de movimento para m1 e m2 são:
Reescrevendo:
Logo, x2 oscila com uma frequência de:
Para reduzirmos o sistema a uma única massa fazemos:
E reescrevemos:
Resposta
Ver passo a passo.