Efetue um cálculo numérico utilizando os parâmetros no Exemplo 10.2 e na Figura 10.4e, determinando a velocidade para a qual a trajetória de movimento passa de volta pela posição inicial no sistema em rotação. Em que tempo o disco sai do carrossel?
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de movimento em um sistema de referência não inercial.
A aceleração efetiva no carrossel é dada pela Equação 10.27:
Essas equações diferenciais acopladas devem ser resolvidas com as condições iniciais:
uma vez que nos é dado no problema que a velocidade inicial faz um ângulo de 45° com o eixo x. Vamos variar v0 em algum intervalo que sabemos que satisfaz a condição de que o caminho se cruze (x0, y0). Podemos começar olhando as Figuras 10-4e e 10-4f, que indicam que queremos v0 > 0,47 m/s.
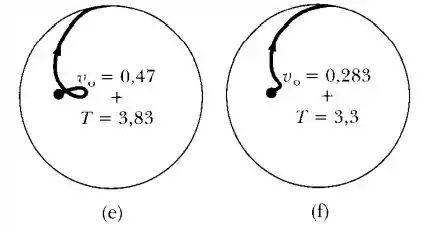
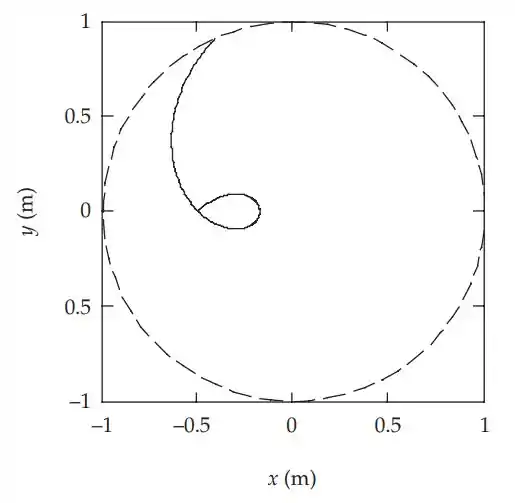
Tentativa e erro podem encontrar uma trajetória que faz um loop, mas não cruza seu caminho, como v0 = 0,53 m/s. A partir daqui, pode-se continuar a resolver diferentes valores de v até que o cruzamento desejado seja adequado ao globo ocular. Esta pode ser uma resposta inteiramente satisfatória, dependendo das inclinações do instrutor. Uma interpolação sobre várias trajetórias mostraria que uma resposta precisa para o problema é v0 = 0,512 m/s, que sai do carrossel em 3,746 s. A figura mostra esta solução, que foi integrada numericamente com 200 passos ao longo do intervalo de tempo.
Resposta
Ver passo a passo.