Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 3.3 - Ex. 4

Um eixo de aço vazado ACB de diâmetro externo 50 mm e diâmetro interno 40 mm está preso contra rotação nas extremidades A e B (veja a figura). As forças horizontais P são aplicadas nas extremidades de um braço vertical que está soldado ao eixo no ponto C.

Determine o valor admissível das forças P se a máxima tensão de cisalhamento permitida no eixo for de 55 MPa. (Dica: Use as Equações 3.46a e b do Exemplo 3.9 para obter os torques de reação).

Passo 1

Fala galera, nesse exercício vamos começar fazendo um D.C.L da parte circular AB considerando binário nos pontos A e B.

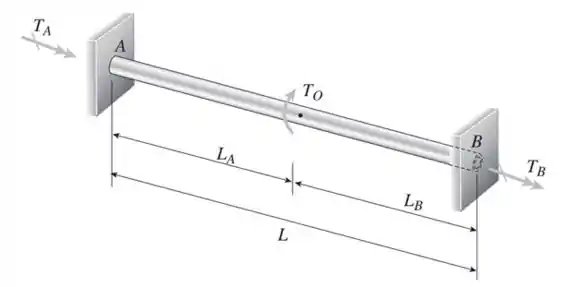
Logo pode se perceber que assumiremos que o torque no eixo é T 0 .

Passo 2

Para o calculo do torque atuando no ponto C , temos

T 0 = F × d

Substituindo

T 0 = P × ( 600   m m )

Passo 3

Iremos calcular o torque reativo nos pontos A e b

T A = T 0 L B L

Substituindo os valores

T A = P × 400   m m × ( 600   m m   ) 1500   m m

T A = 0.16   P

Passo 4

Iremos calcular o torque reativo no ponto B

T B = T 0 L A L

Substituindo os valores

T B = P × 400   m m × ( 900   m m   ) 1500   m m

T B = 0.24   P

Faz se a comparação das duas equações T A   e   T B para poder obter o maior valor do torque.

Sendo assim podemos perceber que o T B   é o maior , logo podemos concluir que :

T m á x   = 0.24   P

Passo 5

Iremos escrever a equação para a tensão de cisalhamento máxima no eixo

τ m á x = T m á x   ( d 2 / 2 ) I p

Substituindo

τ m á x = 0.24   P d 2 2 π 32 d 2 4 - d 1 4

P = τ m á x ( π d 2 4 - d 1 4 3.84 d 2

Substituindo os valores numéricos

P = 55   M P a × 10 6 N / m 2 1   M P a × π 50   m m × 10 - 3 m 1   m m 4 - 40   m m × 10 - 3 m 1   m m 4 3.84 × 50   m m × 10 - 3 m 1   m m

P = 3.320   N

Resposta

Portanto, o valor permitido da força é de 3.320   N .