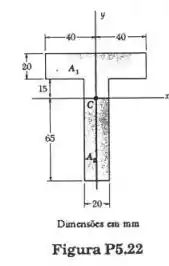
O eixo, horizontal, passa pelo centroide C da superfície da figura e a divide em duas partes e . Determine o momento estático de cada parte componente em relação ao eixo x e explique os resultados obtidos .
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
Já vamos iniciar desenhando a figura mostrando os componentes
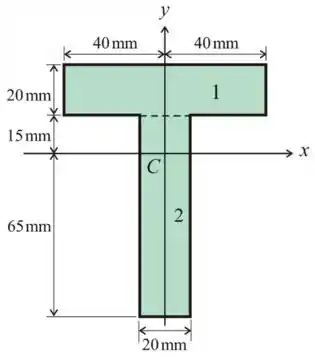
Passo 2
Considerando o componente acima do eixo centroidal como 1 e o componente abaixo do eixo centroidal como 2.
Vamos calcular o primeiro momento de inércia, conhecemos a fórmula como:
Para o componente 1
Portanto, o primeiro momento de inércia para o componente 1 é .
Passo 3
Para o componente 2
Portanto, o primeiro momento de inércia para o componente 2 é .
Resposta
Portanto, o primeiro momento de inércia para o componente 1 é .
Portanto, o primeiro momento de inércia para o componente 2 é .