Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 5.5 - Ex. 6

Um eixo de vagão de carga AB é carregado como mostrado na figura , com as forças P representando as cargas do carro (transmitidas através das caixas de eixo ) e as forças R representando as cargas dos trilhos (transmitidas através das rodas). O diâmetro do eixo é d = 80   m m , a extensão da roda é L = 1.45   m e a distância entre as forças P e R é b = 200   m m .

Calcule a tensão fletora máxima σ m á x no eixo se P = 46,5   k N .

Passo 1

E ai meus amoreess tudo na paz??

Bora?

Primeiro passo e desenhar o diagrama de corpo livre do eixo do vagão de carga, conforme mostrado abaixo:

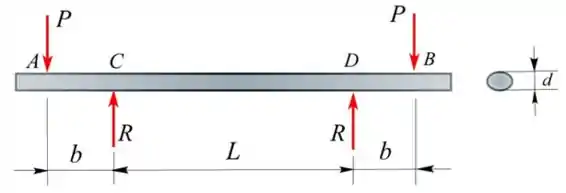
Passo 2

O momento fletor máximo ocorre igualmente em C ou D, onde as cargas ferroviárias são transmitidas ao eixo através das rodas.

Calcularemos o momento fletor máximo no eixo.

M m á x = P × b

M m á x = 46.5   k N × 0.20 m

M m á x = 9.3   k N ⋅ m

Passo 3

Calcularemos o momento de Inércia em torno do eixo neutro da seção transversal.

I = π 64 × d 4

Vamos substituir os dados que o enunciado nos forneceu

I = π 64 × 0.080 4

I = 2.01062 × 10 - 6   m 4

Passo 4

Escreveremos a equação para calcular a tensão máxima de flexão.

σ m á x = M m á x I × c

Onde c é a distancia do eixo neutro à fibra externa da seção transversal

Fazendo as devidas substituições

σ m á x = 9.3   k N 2.01062 × 10 - 6   m 4 × 0.080 2

σ m á x = 185.018   M P a

Portanto, a tensão de flexão máxima no eixo é de σ m á x = 185   M P a   .

Resposta

Portanto, a tensão de flexão máxima no eixo é de σ m á x = 185   M P a   .