Enunciado
Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 7.2 - Ex. 1
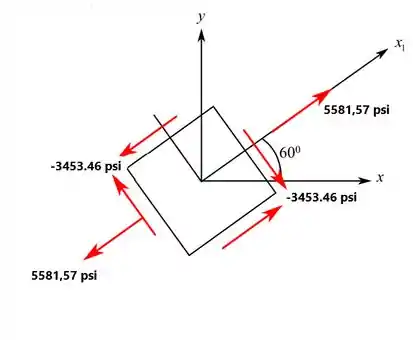
Um elemento em tensão plana está submetido a tensões , , , como ilustrado na figura.
Determine as tensões agindo em um elemento orientado a um ângulo a partir do eixo , em que o ângulo é positivo quando está no sentido horário. Mostre essas tensões em um esboço de um elemento orientado ao ângulo .
Passo 1
EAIIII PEXUAAAALLL!!
Determinaremos a tensão normal atuando em face do elemento orientado em ângulo a partindo do , usando as equações de transformação da seguinte maneira:
Fazendo as devidas substituições
Portanto, a tensão normal atuando em face do elemento orientada em um ângulo de com eixo é de
Passo 2
Determinaremos a tensão de cisalhamento que atua no elemento orientado no ângulo do eixo x, usando as equações de transformação
Substituindo os devidos valores:
Portanto, a tensão de cisalhamento no plano inclinado é de .
Passo 3
Esboce a orientação do elemento e mostre as tensões atuando no elemento
