Encontre os modos normais para os pêndulos acoplados na Figura 12.5 quando o pêndulo à esquerda possui cabeça de massa e o da direita possui cabeça de massa . O comprimento de ambos os pêndulos é de 40 cm e a constante cla mola é 0,020 N/m. quando o pêndulo da esquerda é inicialmente puxado de volta a e liberado do descanso quando, qual é o ângulo máximo que se alcança? Utilize a aproximação do ângulo pequeno.
Passo 1
Bora lá pessoal, vamos começar com as energias.
Energia cinética:
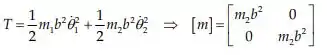
Energia potencial:
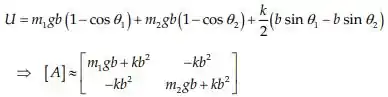
Passo 2
Resolvendo a equação, , que nos dá as frequências de oscilação apropriadas.
![]()
A autofrequencia correspondente a é com .
A autofrequencia correspondente a é com .
Passo 3
E olha aí da solução do problema 12-27, nós temos que as coordenadas normais são:
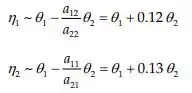
Pega essa visão, com isso percebemos que caracteriza a oscilação em fase de dois pêndulos, e caracteriza a oscilação fora de fase de dois pêndulos.
Passo 4
Agora, para incorporar as condições iniciais, vamos escrever a forma de oscilação mais geral:
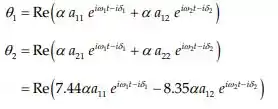
onde é uma constante de normalização real. As condições iniciais ajudam a determinar os parâmetros .

Como então:
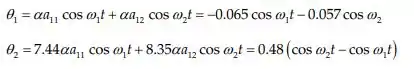
Onde e :
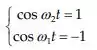
Resposta
E seguindo o jogo, vemos que o ângulo máximo é aproximadamente 0,096 e isso acontece quando:
Que nos dá:
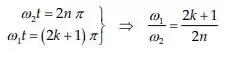
Como encontramos e .