Encontre a relação entre o raio e a distância para a área composta mostrada na figura, de forma que o produto de inércia seja zero.
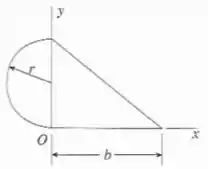
Passo 1
Bora lá galera!
Começando pelo triângulo, temos que:
E agora para o semicírculo, ficamos com o seguinte produto de inércia:
Dados:
Portanto,
Passo 2
Com isso my friends, basta somarmos os produtos de inércia e igualarmos a zero para demonstrar a relação entre o raio e a distância , logo:
Essa questão foi, heim... Bora pra próxima?