A energia de um quantum de luz (ou fóton) é expressa por onde é a constante de Planck e é a frequência do fóton. A quantidade de movimento do fóton é . Mostre que, se o fóton espalha a partir de um elétron livre (de massa ), o fóton espalhado tem uma energia:
Onde é o ângulo por meio do qual o fóton espalha. Mostre também que o elétron adquire uma energia cinética:
Passo 1
Faala meu povo, bora com tudo para a ÚLTIMA questão do nosso livro!
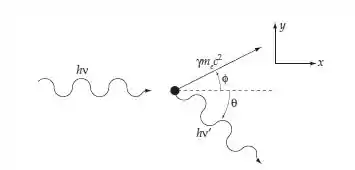
Da conservação da energia, temos:
A conservação do momento ao longo do eixo dá:
A conservação do momento ao longo do eixo fornece:
Para eliminar , usamos (2) e (3) para obter:
Então:
Desde e , teremos:
Substituindo de (1) em (6), temos:
De (5) e (7), podemos encontrar a equação para :
Ou,
Então,
Ou,
A energia cinética do elétron é:
Finalizamos aqui nossa questão, tranquilo? Te vejo na próxima!