Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 7.Problemas - Ex. 3

Uma esfera de raio ρ é restrita para rodar- sem deslizamento na parte inferior da superfície interna de um cilindro oco de raio interno R. Determine a função de Lagrange, a equação de restrição e as equações de movimento de Lagrange. Encontre a frequência de pequenas oscilaçóes.

Passo 1

Faaaaaala, galera... Tranquileba??

Limpe as sandálias dos seus pés, que as equações lagrangianas são sagradas pra física.

Fazendo um esboço da situação, temos:

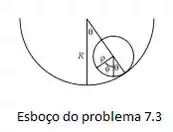
Onde nós temos pela função lagrangiana:

L = K - U

Onde a energia cinética deve levar em conta o movimento e rotação, assim:

K = 1 2   m   x ' 2 + 1 2   I   ϕ ' 2

Sendo I 0 momento de inercia da esfera, I e s f e r a = 2 5   m   ρ 2

Sendo L o comprimento R - ρ

E:

y = [ R - R - ρ cos ⁡ θ   ]

Assim temos:

K = 1 2   m R - ρ θ ' 2 + 1 2   I   ϕ ' 2

U = m g y = m g [ R - R - ρ cos ⁡ θ   ]

Assim:

L = 1 2   m R - ρ θ ' 2 + 1 5   m   ρ 2   ϕ ' 2 - m g R - R - ρ cos ⁡ θ                 ( 0.1 )

Bora pro próximo passo?!

Passo 2

Obrigado por vir.

A equação 0.1 nos dá a equação de restrição:

f θ , ϕ   = R - ρ θ - ρ ϕ = 0

Passo 3

Usando as equações de Lagrange (Com um multiplicador indeterminado de correção):

∂ L ∂ θ   - d d t ∂ L ∂ θ ' + λ ∂ f ∂ θ = 0 ∂ L ∂ ϕ   - d d t ∂ L ∂ ϕ ' + λ ∂ f ∂ ϕ = 0  

Já temos logo de cara que ∂ f ∂ θ = R - ρ e ∂ f ∂ ϕ = - ρ e introduzindo L temos:

- R - ρ m g   sin ⁡ θ - m R - ρ 2 θ ' ' + λ R - ρ = 0

- 2 5   m ρ 2 ϕ ' ' - λ ρ = 0

Pela ultima, sabemos que:

λ = 2 5   m ρ ϕ ' '

Ou da equação de restrição:

λ = 2 5 m R - ρ θ ' '

Assim, retornando a substituição:

- R - ρ m g   sin ⁡ θ - m R - ρ 2 θ ' ' + 2 5 R - ρ θ ' ' m R - ρ = 0

θ ' ' 2 5 m R - ρ 2 - m R - ρ 2 - R - ρ m g sin ⁡ θ = 0

θ ' ' 2 5 m R - ρ 2 - m R - ρ 2 = R - ρ m g sin ⁡ θ

θ ' ' R - ρ 2 2 5 m - m = R - ρ m g sin ⁡ θ

θ ' ' = m g sin ⁡ θ 2 5 m + m R - ρ = 5 g 7 R - ρ sin ⁡ θ

Com ω 2 =   5 g 7 R - ρ  

Resposta

Ei, a resposta está no passo a passo :)