A Figura 3.8 ilustra uma massa impelida por uma força senoidal cuja frequência é . A massa é presa a um suporte rígido por meio de um fio de constante de força e desliza sobre uma segunda massa , A força de atrito entre e , é representada pelo parâmetro de amortecimento , e a força de atrito entre e o suporte é representada por . Construa o análogo elétrico desse sistema e calcule a impedância.
Passo 1
Faala meu povo, bora com tudo pra mais uma questão do nosso livro!
Bem galerinha essa questão é muito boa, então vem comigo, para construir o análogo elétrico deste sistema mecânico, primeiro precisamos escrever as equações de movimento para este sistema:
Para a massa , nós temos:
Para a massa , nós temos:
Usando a tabela 3-1 do nosso livro.
Obtemos as seguintes equações:
E
Dessa forma, o circuito elétrico resulta em:
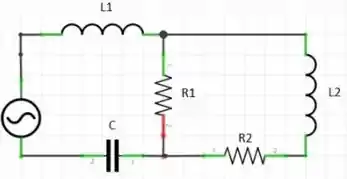
A impedância total , é:
Assim temos:
Finalizamos aqui nossa questão, tranquilo? Te vejo na próxima!