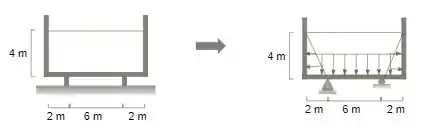
 A figura seguinte apresenta corte transversal de um reservatório paralelepipédico preenchido de água. Com a idealização de um segmento transversal de largura unitária desse reservatório como pórtico plano com apoios articulados, como mostra a parte direita dessa figura, pede-se determinar os diagramas de momento fletor e de esforço cortante.
A figura seguinte apresenta corte transversal de um reservatório paralelepipédico preenchido de água. Com a idealização de um segmento transversal de largura unitária desse reservatório como pórtico plano com apoios articulados, como mostra a parte direita dessa figura, pede-se determinar os diagramas de momento fletor e de esforço cortante.
Passo 1
Em um primeiro momento devemos calcular a carga distribuída sobre as paredes do reservatório, este valor pode ser obtido através da fórmula de pressão em fluídos, utilizando e a gravidade como ;
Sendo assim, este é o valor que utilizaremos para a carga distribuída, considerando que a única carga aplicada sobre as paredes será a pressão exercida pela coluna de água.
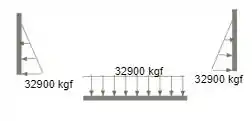
Passo 2
Para determinarmos os respectivos diagramas devemos levar em conta as reações de apoio na estrutura, como determinadas abaixo.
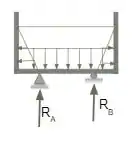
Para isso devemos levar em conta as equações de equílibro das forças horizontais, verticais e do momento.
Agora para definirmos o momento temos que considerar novamente a equação de equílibro.
Agora substituimos o valor encontrado para RB na equação de equílibro encontrada nas forças horizontais.
Passo 3
Para construir os diagramas de esforço cortante, devemos fazer os balanços verticais por seção, indo de 0 até a seção. Considerando V(x) o valor do esforço cortante na posição x e sendo representado pelas flechas na imagem abaixo.
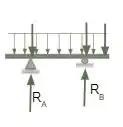
Considerando a seção 1, , da viga, temos:
Já para a segunda parte da seção, , temos:
Para a última seção da viga , temos
Como temos um pórtico, devemos realizar o mesmo passo para as paredes do pórtico.

Neste caso, temos somente uma seção , sendo assim:
No outro lado do pórtico temos a mesma condição, porém com as forças contrárias sendo assim a equação do diagrama de força cortante, será a mesma, porém com o sinal invertido.
Sendo assim o diagrama de forças, será:

Passo 4
Para realizar o diagrama de momento fletor, temos que fazer o balanço de momento em cada seção, em que M(x) é o valor do momento em x, ou seja:
- Assim como antes começaremos pela viga do pórtico, definindo a primeira seção como
- Agora na segunda seção
- Já na última seção temos
Assim como no diagrama de esforça cortante, temos que realizar também os da parede, como uma só seção .
No outro lado do pórtico temos a mesma condição, porém com as forças contrárias sendo assim a equação do diagrama de força cortante, será a mesma, porém com o sinal invertido.
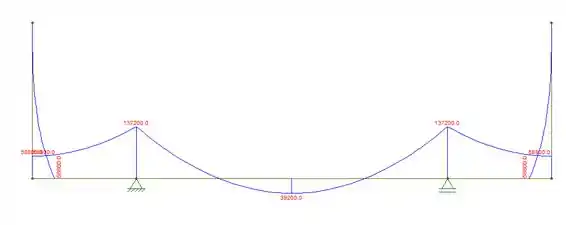
Resposta
Ei, a resposta está no passo a passo :)