Um fio é puxado para o lado a uma distância h em um ponto a partir de uma extremidade. Em um ponto da outra extremidade, o fio é puxado para o lado a uma distância h na direção oposta. Discuta as vibrações em termos de modos normais.
Passo 1
Faaaaaala, galera... Tranquileba??
Saca só, façamos um esboço da situação dita, temos:
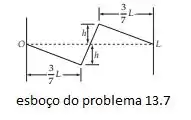
Como dito, a condição inicial é:
E as equações que determinam os modos normais de vibração é:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim:
E para
Passo 3
Calculando para , temos:
Onde o modo normal dependerá de r
Resposta
Onde o modo normal dependerá de r