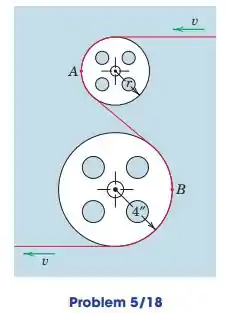
A fita magnética está sendo alimentada sobre e ao redor da luz polias montadas em um computador. Se a velocidade v do fita é constante e se a magnitude da aceleração do ponto A na fita é 4/3 vezes a do ponto B, calcule o raio r da polia menor.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Tomemos as componentes tangenciais da aceleração nos pontos A e B como zero porque a velocidade da fita é constante
Escrevendo as expressões das acelerações normais do sistema dado nos pontos A e B, temos
Onde,
A velocidade da fita é V.
O raio da polia pequena é r.
O raio da polia grande é R.
Passo 2
Dividindo ambas as acelerações nos pontos, temos
Pra R igual a 4”, temos
Resposta
Portanto, o raio da polia menor é ;