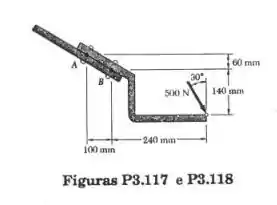
Uma força de é aplicada À placa dobrada da figura. Determine : (a) um sistema força-binário equivalente em A e (b) um sistema equivalente formado por forças paralelas aplicadas em A e B.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
- Sistema força-binário equivalente em A.
- Sistema equivalente formado por forças paralelas atuando em A e B.
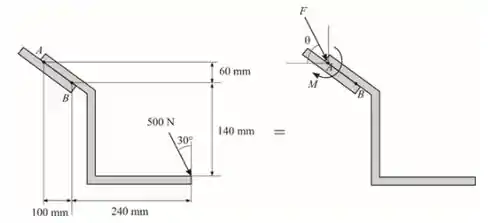
Passo 2
A soma da força ao longo do eixo x deve ser a mesma para ambos os casos
A soma da força ao longo do eixo y deve ser a mesma para ambos os casos
Igualando as equações (1) e (2);
Da equação (1)
Portanto, a força do sistema força-binário em A é .
A soma dos momentos em relação a A deve ser a mesma para ambos os casos
Portanto, o momento do sistema força-binário em A é
Passo 3
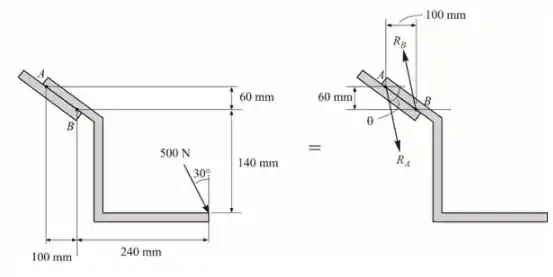
São duas forças paralelas em A e B, temos ângulo feito pela força paralela com eixo horizontal é
A soma da força ao longo do eixo deve ser a mesma para ambos casos
Soma dos momentos em relação a A deve ser a mesma para ambos os casos
Portanto, a força paralela equivalente em B é de
Partindo da expressão (3), iremos obter
Portanto, a força paralela equivalente em A é
Resposta
- Portanto, o momento do sistema força-binário em A é
- Portanto, a força paralela equivalente em A é