A força F, de intensidade igual a 500 N, é decomposta em duas componentes segundo as direções a-a e b-b-. Determine, por trigonometria, o ângulo , sabendo que a componente de F ao longo da linha a-a é de 400 N.
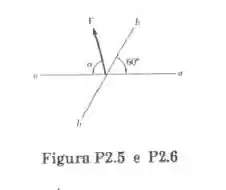
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
A magnitude da força,
A componente da força F ao longo da linha
Diagrama das forças
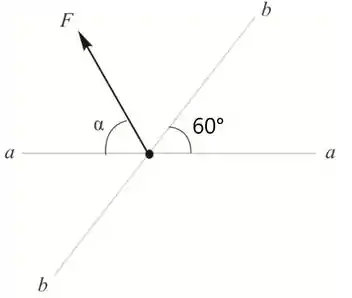
Passo 2
O triangulo da força é
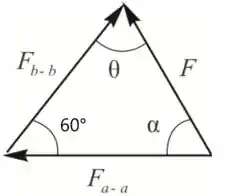
Passo 3
Do triangulo de forças, temos:
Aplicando a regra dos senos,
Portanto,
Portanto, o ângulo entre a força para a seção é
Resposta
Portanto, o ângulo entre a força para a seção é