Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 5.5 - Ex. 5

Uma gangorra que pesa 4 lb/ft de comprimento é ocupada por duas pessoas, pesando 80lb cada (veja a figura). O centro de gravidade de cada criança está a 8,5 ft do ponto de apoio da alavanca. A tábua tem comprimento de 20 ft, 9 in, de largura e 1,6 in, de espessura.

Qual é a tensão fletora máxima na tábua?

Passo 1

Falaaa meus consagradx’sss beleuzaaaaa??

Simboráaaa

Iremos partir do diagrama de corpo livre

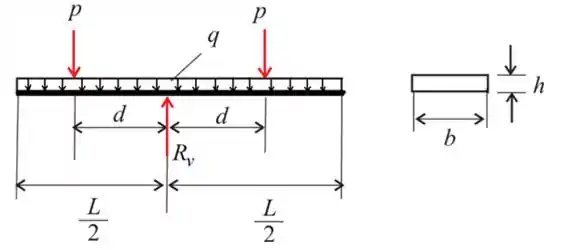
Onde

R v é a reação vertical no fulcro

(OBS: fulcro e uma base, ponto de apoio).

Passo 2

O momento fletor máximo estará atuando no fulcro, pois o carregamento é simétrico.

Considere a metade esquerda da gangorra a partir do fulcro.

Momento de flexão máxima.

M m á x = p × d + q × L 2 × l 2 2

M m á x = p × d + q × L 2 × L 2 1 2

M m á x = p × d + 1 2 q L 2 2

Substituindo os dados fornecidos pelo enunciado, iremos obter:

M m á x = 80 × 8.5 + 1 2 × 4 × 20 2 2

M m á x = 680 + 200

M m á x = 880   l b ⋅ f t

Passo 3

Iremos encontrar o módulo de seção do retângulo usando a seguinte expressão:

S = I y m á x

S = I h 2

Vamos substituir o I por 1 12 b h 3

S = 1 12 b h 3 h 2

S = 1 12 b h 3 × 2 h

S = b h 2 6

Substituindo os valores dados pelo enunciado

S = 9 × 1 , 6 2 6

S = 3.84   i n 3

Passo 4

Iremos encontrar agora a tensão de flexão máxima usando a seguinte expressão:

σ m á x = M m á x S

Calcule a tensão máxima de flexão na placa.

σ m á x = M m á x S

Substituindo os valores do enunciado e os obtidos ao longo da resolução

σ m á x = 880   l b ⋅ f t × 12 i n f t 3.84   i n 3

σ m á x = 2.750   p s i

Resposta

Portanto, a tensão máxima de flexão na placa é de 2.750 psi.