A haste dobrada tem uma massa de 3 kg/m. Determine o momento de inércia da barra em relação ao eixo O-a.
Passo 1
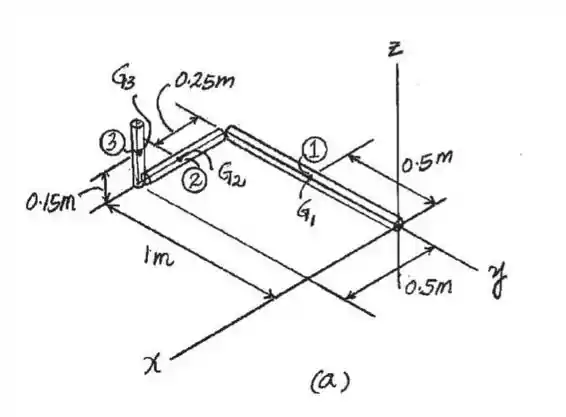
A haste dobrada é subdividida em três segmentos e a localização do centro de massa para cada segmento é indicada na Fig. a. A massa de cada segmento é , e .
Passo 2
O vetor unitário que define a direção do eixo é
Por isso
Passo 3
Então