Idem para os arcos representados que se seguem:
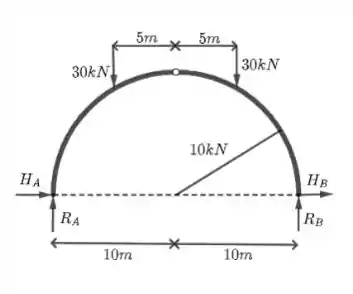
Passo 1
Nesse caso, temos quatro incógnitas que são as reações verticais e horizontais tanto em A e B. Entretanto, devido à rótula C, temos uma equação de equilíbrio a mais que nos permite determinar a incógnita adicional. Assim, vamos calcular os momentos das forças do arco todo em relação ao ponto A e do semi-arco BC em relação ao ponto C.
Além das forças de reação, temos duas forças de módulo , uma atuando a de A e outra atuando a de A ( de C).
Passo 2
As duas equações de equilíbrio dos momentos nos dão:
Agora, podemos obter as demais reações: